①风险偏好理论
不同的实验者对风险的态度是存在差异的,一部分人可能喜欢大得大失的刺激,另一部分人则可能更愿意“求稳”,根据实验参与投资提对风险的偏好差异,将其分为保守型、稳健型、平衡型、成长型、进取型。本实验中面向实验者进行交互式的风险问卷调查,自动判定实验者投资风险偏好类型与对应等级,并将风险偏好类型代入映射到后续家庭投资组合的测算与风险智能预警。
②投资组合风险分析
投资组合是由投资人或金融机构所持有的股票、外汇、债券、外汇以及金融衍生产品等组成的集合,目的是分散风险。假设由$$\mathrm{N}$$只股票构成一个投资组合,各只股票的预期收益率分别为$$\mathrm{E(R_i)}$$,其对应的配置权重为$$\mathrm{{\scriptsize
W_i} } $$,则投资组合的预期收益率$$\mathrm{E(R_p)}$$如下:
$$E(R_p)=\sum_{i=1}^NW_iE(R _i)=[{\scriptsize W_1,W_2,\cdots
W_N}][E(R_1),E(R_2),\cdots ,E(R_N)]^T$$
投资组合的收益率方差$$\sigma ^2_p$$计算表达式如下:
$$\sigma^2_p=\sum\sum {\scriptsize W_iW_j}COV (R_i,R_j)=\sum\sum {\scriptsize
W_i}{\scriptsize W_i} \rho_{ij} \sigma_i\sigma_j=W\sum W^T $$
$$\sum = \left[ \begin{array}{}
\sigma^2_1 & \sigma_{12} & \cdots & \sigma_{1N} \\
\sigma_{21} & \sigma^2_2 & \cdots & \sigma_{2N} \\
\vdots & \vdots & \cdots & \vdots \\
\sigma_{N1} & \sigma_{N2} & \cdots & \sigma^2_N \\
\end{array} \right] , \rho_{ij}=\frac{COV(R_i,R_j)}{\sigma_i \sigma_j}$$
波动率(标准差)近似遵循平方根法则,可以通过日收益波动率进行月度或年度的波动率测算,分别为:
$$\sigma_{month} = \sqrt[]{22}\sigma_{day} $$
$$\sigma_{year} = \sqrt[]{252}\sigma_{day} $$
③有效前沿分析
投资组合中的权重变量可以实现投资组合的预期收益率与波动率之间的映射。在投资组合理论中,所有可能的投资组合被称为可行集(Feasible Set),有效前沿(Efficient
Frontier)是可行集的一条包络线,它表示在不同风险条件下能够给投资者带来的最高预期收益率,或者在不同预期收益率条件下能够给投资者带来的最低波动率,有效前沿分析即求解以下最优化问题:
$$ \min_{{\scriptsize W_i}}\sigma_p=\min_{{\scriptsize
W_i}}\sqrt{{\scriptsize W_iW_j}Cov(R_i,R_j)} $$
$$ s_.t:\sum_{i=1}^{N}{\scriptsize W_i}=1,{\scriptsize W_i} >0 $$
$$ E(R_p)=E(\sum_{i=1}^{N}{\scriptsize W_i}R_i)=给定常数 $$
其中,约束条件$${\scriptsize W_i>0}$$表明资本市场不允许卖空,即实验者不允许融券操作。
④资本市场线
将无风险资产引入投资组合,也就意味着投资者可以按照无风险利率借入或借出资金,这样就引出了一条重要的曲线—资本市场线。资本市场线(Capital Market
Line,CML)是一条从无风险利率引出的与有效前沿相切的一条切线,并且该切线有且仅有一条,切点对应的投资组合称为市场组合(Market Portfolio)或切点组合(Tangency
Portfolio),资本市场线的数学表达式如下
$$E(R_{p})=R_{F}+[\frac{E(R_{M})-R_{F}}{\sigma_{M} } ]\sigma_{p} $$
其中$$R_F$$代表市场的无风险利率,$$E(R_M)$$与$$E(\sigma_M)$$分别代表市场组合的收益波动率与波动率。
⑤不考虑风险偏好下的最优投资组合
最优投资组合就是测算在所选众多标的产品中,求解每个标的产品的最优配置比例$${\scriptsize
W_i}$$,即求解投资组合中每只股票的最优配置权重,通过求解如下的最大值方程(夏普比率最大化),可得到最优投资组合权重:
$$\max_{{\scriptsize W_i}} \frac{E(R_{p})-R_{F}}{\sigma_{p}} $$
$$s.t:\sum_{i=1}^{N} {\scriptsize W_i}=1,{\scriptsize W_i}>0$$
⑥VaR(风险价值)模型
VaR(处于风险状态的价值),即在一定置信水平和一定持有期内,某一金融工具或其组合在未来资产价格波动下所面临的最大损失额。Jorion把VaR定义为“给定置信区间的一个持有期内的最坏的预期损失”,其公式如下
$$ Prob(\Delta p< - VaR)=1-\alpha $$
其中$$\mathrm{p_t}$$表示$$\mathrm{t}$$时刻的资产组合价值,$$\mathrm{∆P=P_t-P_{(t-1)}}$$为第t期限中的损失,VaR为在险价值,α为置信度。
⑦不同风险偏好下的最优投资组合
实验投资者根据其在前序风险偏好问卷调查环节,计算得到投资风险偏好类型与对应等级,确定其对应的VaR警戒线,不同风险偏好下的最优投资组合测算,即将投资者VaR警戒线引入作为新增的非线性约束条件,不同实验者风险偏好下的最优投资组合问题演变为以下以下最大值问题的求解:
$$\max_{{\scriptsize W_i}} \frac{E(R_{p})-R_{F}}{\sigma_{p}} $$
$$s.t:\sum_{i=1}^{N} {\scriptsize W_i}=1,{\scriptsize W_i}>0$$
$$Prob(\bigtriangleup p <-VaR)=1-\alpha $$
$$VaR < VaR_{max} $$
⑧期望损失ES模型
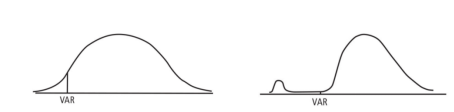
VaR 的局限性导致其不具备度量投资组合尾部风险的能力,它将损失可能发生的概率限定为一个固定值。此外,在采用 VaR 确定风险时,无法捕获金融资产收益率「厚尾风险」的典型特征,因此低估了实际的市场风险。在图 2中,两类资产分布具有相同的VaR数值,却具有明显不同的尾部分布情况,右图资产极端风险更高。
若要度量投资组合损失超过 VaR 损失时所遭受的平均损失程度,更为准确地进行市场风险管理,就需要通过 ES(Expected Shortfall 期望损失)模型来实现。
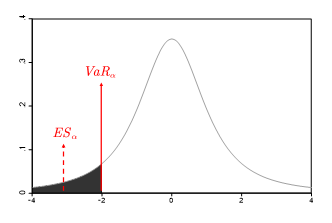
ES定义:当投资组合的损失超过 VaR 损失(例如,图 3所示 α% 的 VaR)时所遭受的期望损失ES(即平均损失的大小)。
$$\mathrm{SR= \frac{E(R_p)-R_F}{\sigma_p } } $$
其中,$$\mathrm{E(R_p)}$$表示投资组合的预期收益率,通常用过往年化收益率代替,
$$\mathrm{E(R_F)}$$表示无风险利率,$$\mathrm{\sigma_p}$$表示投资组合波动率
投资组合承担每一单位风险所带来的超额收益(以风险利率作为比较基准)
索提诺比率
(Sortino Ratio,SOR)
$$\mathrm{SOR= \frac{E(R_p)-R_F}{\sigma_D } } $$
其中,$$\mathrm{\sigma_D}$$代表投资组合收益率的下偏标准差
投资组合承担每一单位下行风险(downside risk)所带来的超额收益
$$ \mathrm{TR= \frac{E(R_p)-R_F}{\beta_p } } $$
其中,$$\mathrm{\beta_p}$$代表投资组合的贝塔值
投资组合每承担一单位系统风险时,会产生多少的风险溢价
信息比率
(Information Ratio,IR)
$$ \mathrm{ID=\frac{TD}{TE}= \frac{E(R_p)-E(R_B)}{TE} } $$
其中,$$\mathrm{E(R_B)}$$表示基准组合的预期收益率,$$\mathrm{TD}$$和$$\mathrm{TE}$$则分别表示跟踪偏离度和跟踪误差(跟踪偏离度波动率)
表示投资组合承担每一单位主动管理风险所带来的超额收益

 板块一
板块一